What Is Atomic Packing Fraction

Atomic Packing Factor (APF) tells you what percent of an object is made of atoms vs empty space. You can think of this as a volume density, or as an indication of how tightly-packed the atoms are.

For quick reference, I have created a table below of atomic packing factor (APF) values for mutual crystal structures. Afterwards in the article, I explain step-by-step how to calculate them.

Crystal Construction	Diminutive Packing Factor
Uncomplicated Cubic (SC)	52%
Body-Centered Cubic (BCC)	68%
Face-Centered Cubic (FCC)	74%
Hexagonal Close-Packed (HCP)	74%

Atomic packing gene (APF) of common crystal structures.

Calculating the atomic packing gene for a crystal is simple: for some repeating book, calculate the volume of the atoms inside and divide by the total book.

$APF=\frac{volume\:taken\:by\:atoms}{total\:volume}$

Usually, this "repeating volume" is merely the book of the unit prison cell. The unit of measurement cell is defined as the simplest repeating unit of measurement in a crystal.

Bold all atoms have the same size, and are arranged in a repeating crystal lattice,

$APF=\frac{N_{atoms}V_{atom}}{V_{unit\:cell}}$

where $N$ means number and $V$ means volume.

For a more complicated description of having multiple kinds of atoms, click here to aggrandize.

If you have multiple kinds of atoms, y'all need to include the number and volume of each atom.

$APF=\frac{\sum _iN_iV_i\:\:}{\:V_{total}}$

where $V_i$ is the volume of each type of cantlet. In metals there is usually only one atom, merely in a ceramic, suppose at that place are 3 kinds of atoms: $A$ , $B$ , and $C$ . The expanded version would await like this:

$APF=\frac{N_AV_A+N_BV_B+N_CV_C\:}{\:V_{unit\:cell}}$

Additionally, atomic packing factor uses the hard sphere model. That means each cantlet has the volume of a sphere. Assuming the atoms are hard spheres with radius $r$ in a cubic unit prison cell with lattice parameter $a$ ,

$APF=\frac{\frac{4}{3}\pi \:r^3\cdot N_{atoms}}{a^3}$

This might be a footling hard to conceptualize, so let's commencement by dropping into one- and two-dimensions.

1-Dimensional Packing Factor: Linear Density

Since we're in 1D, formulas with volume don't utilise. Don't worry! If you sympathize the concept, y'all won't need a formula at all.

Remember, nosotros want to find the space taken by atoms compared to the total infinite. Since we're in one-dimension, "infinite" means "length." We tin say that 1-dimensional packing is a linear density or line density.

For any detail direction, you need to draw a line and decide what percent of the line is covered by a circle.

Of grade, you can't just draw whatsoever random line. The line needs to be along the crystal "cell."

If you lot're non sure how to do this in 1-dimension, click here to expand.

This picture may brand it seem like the unit jail cell is simply an atom, but that's only true in the close-packed direction. Usually, it makes the nigh sense to describe the unit of measurement cell so that a half-atom sticks out on both ends (like the red unit cell).

See, if the atoms are not "shut-packed," the unit cell will need to take more space. In other words, the lattice will exist larger than the footing.

(In the arrangement above, the lattice and basis are the same size, which is why you define the unit of measurement prison cell effectually the circle with no actress space).

As long as the line yous draw is a valid representation of the overall crystal symmetry, any line will work!

Simply take the length of the line covered past circles, and divide past the total length of the line.

The maximum packing cistron is ane, which means 100% of the line is occupied past a circle.

If you had a packing factor larger than i, it would mean that somehow multiple circles overlapped on the same section of the line.

2-Dimensional Packing Factor: Planar Density

In ii dimensions, infinite is area, rather than a line or a volume. Determining the packing factor works exactly the aforementioned way, nevertheless. Nosotros telephone call this the planar density or area density.

Simply find a crystallographically repeating area (the unit cell will ever work) and divide that area past the area covered by the circles.

Wait at that! These two arrangements have the aforementioned packing. Any idea why that is . . . ?

At present, let's move into three dimensions and take a look at how to summate APF for the 4 mutual unit of measurement cells.

Simple Cubic (SC) Lattice Length and APF

As before, we desire to know how much of the crystal space is occupied by atoms vs empty space. Nosotros accept entered 3-dimensions (the real world), so space is book. To perform this adding, we need to know the volume of a cube and the book of a sphere.

Volume of a cube: $V_{cube}=a^3$ , where $a$ is the length of a side.

Book of a sphere: $V_{sphere}=\frac{4}{3}\pi r^3$ , where $r$ is the radius of the sphere.

At present, nosotros have 2 variables: $r$ (radius of atom) and $a$ (side length of cube).

It turns out that $r$ and $a$ can be written in terms of each other.

A elementary cubic (SC) unit of measurement jail cell is a cube with an atom on each corner of the cube. The size of the cube will be adamant past the size of the atoms!

Equally you tin see, for the simple cubic cell, the lattice parameter is just twice the radius. Now, in terms of the radius, we can say that the volume of the cube is:

Each atom is a sphere, then the volume per atom is:

$V_{sphere}=\frac{4}{3}\pi r^3$

where $r$ is the radius of the sphere.

But, how many atoms practice we take per unit prison cell? At first glance, it looks like there are 8 atoms: on on each corner of the cell.

Notwithstanding, you need to consider that when you stack unit of measurement cells to make the full crystal, each corner is shared with 8 cells. So each of the 8 atoms contributes ⅛ of its total book. In total, at that place is 1 total atom per unit cell.

Now if we split up the book of an cantlet by the book of the unit cell, the atomic packing factor for a simple cubic crystal is:

$APF_{SC}=\frac{\frac{8}{8}\cdot \frac{4}{3}\pi r^3}{^{\left(2r\right)^3}}=\frac{\pi }{6}\approx 52\%$

Trunk-Centered Cubic (BCC) Lattice Length and APF

To calculate the atomic packing cistron, what do we demand first? The volume of the atoms, and the book of the unit of measurement cell.

For some radius of the atoms, nosotros can calculate their volume using

$V_{sphere}=\frac{4}{3}\pi r^3$

The volume of the cube is $a^3$ in terms of the lattice abiding $a$ , and so let'due south write $a$ in terms of $r$ .

In a BCC crystal, the body diagonal is the shut-packed direction. I hope this is articulate in the prototype below.

Since the body diagonal is the shut-packed direction, the atoms affect each other. That means the body diagonal will be a multiple of the diminutive radius. In this case, the torso diagonal is $4r$ .

Now, it's time to employ the pythagorean theorem (you could also use 3D vector math, but if you don't know what that is, the trigonometry is not and so complicated).

First, brand a triangle with the body diagonal every bit the hypotenuse. This is the green line in the image above. One of your triangle legs volition be the cube'southward side, $a$ . The other leg will exist the face diagonal. Yous tin can utilise whatever variable you lot like for this length; I volition choose $d$ .

Using the pythagorean theorem, $a^2+d^2=(4r)^2$ .

Now, let's find $d$ . We can make another triangle from a dissimilar 3D view; this fourth dimension our triangle has $d$ on the hypotenuse and $a$ for both legs.

Again using the pythagorean theorem, nosotros see $a^2+a^2=d^2$ , or $d^2=2a^2$ .

At present nosotros can plug $d^2$ into our commencement pythagorean theorem.

So,

$a=\frac{4}{\sqrt{3}}r$

At present that nosotros can write the volume of the cube in terms of the diminutive radius, the balance is easy!

We but demand to figure out how many atoms are in each unit cell. Equally in the simple cubic example, in that location are 8 corner atoms. Each corner cantlet contributes ⅛ of its volume to the unit of measurement cell, so that'due south equal to 1 whole cantlet.

Additionally, there is an atom in the eye of the cell. Since that entire atom is inside the cell, it fully contributes its volume.

In total, there are 2 atoms in the BCC unit of measurement cell. If we divide the volume of ii atoms by the book of the unit cell ( $=a^3$ ), nosotros find that the atomic packing factor for a body-centered cubic crystal is:

$APF_{BCC}=\frac{\left(\frac{8}{8}+1\right)\frac{4}{3}\pi \:r^3}{\left(\frac{4}{\sqrt{3}}r\right)^3}=\frac{\sqrt{3}\pi }{\:8}\approx 68\%$

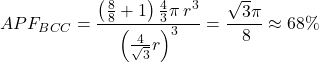
Face-Centered Cubic (FCC) Lattice Length and APF

This should exist familiar by at present. Book of the atoms divided by volume of the unit cell. Let's get the unit jail cell in terms of the atomic radius!

In an FCC crystal, whatever face diagonal is the shut-packed direction. I hope you tin can see this in the paradigm below.

The face diagonal, therefore, has a length of $4r$ . We can get the lattice constant in terms of $r$ with a simple application of the pythagorean theorem.

Describe a triangle with the face diagonal (length = $4r$ ) as the hypotenuse. Both legs will exist $a$ .

And so $a=2\sqrt{2}r$

$a^3$ will be the volume of the unit cell, so let's effigy out how many atoms are in the unit cell.

Equally nosotros've seen several times already, there will be 8 atoms on each corner, each contributing ⅛ of its total book to the unit jail cell.

Additionally, in that location are half-dozen faces, with half an cantlet on each confront (since faces are shared between two cells, an atom on the face up would contribute ½ of its volume to each cell).

In full, there are 4 atoms in the FCC unit cell. Dividing the volume of four atoms by the volume of the cube gives united states of america the atomic packing gene for a face-centered cubic crystal:

$APF_{FCC}=\frac{\left(\frac{8}{8}+\frac{6}{2}\right)\frac{4}{3}\pi r^3}{\left(2\sqrt{2}r\right)^3}=\frac{\pi }{3\sqrt{2}}\approx 74\%$

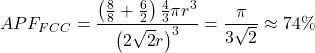
Hexagonal Shut-Packed (HCP) Construction and APF

At present things become tricky.

The HCP crystal construction is not cubic. Luckily, it's all the same relatively like shooting fish in a barrel to visualize. It's the natural fashion for humans to pack spheres.

Imagine you had to pack spheres into a box. You'd probably get-go by making a close-packed aeroplane on the lesser of the box. Then, you'd start the next airplane by placing a sphere at one off the depression points–in between 3 spheres from the bottom airplane. Again, the 2d plane tin can be arranged equally close-packed. The tertiary plane would wait exactly like the 1st plane, the 4th plane would look exactly like the 2nd airplane, so on.

This is the hexagonal shut-packed lattice!

We call this unit cell "hexagonal shut-packed" because it looks like hexagonal planes. In nigh all cases, nosotros use the full HCP prison cell.

Yet, it's actually possible to define a smaller unit cell from the same atomic system. This is a rhombohedral cell. Since this is the smallest unit of measurement cell possible, we call this the HCP primitive unit of measurement cell.

Let's expect at the primitive unit of measurement jail cell, because it'due south simpler so information technology'south piece of cake to run across the lattice parameters. Unlike a cube, at that place are really 2 independant lattice parameters.

Lattice parameter $a=b$ is the length between 2 touching atoms (so, twice the radius).

Lattice parameter $c$ is the height of the unit prison cell.

By taking advantage of some trigonometry, information technology turns out that in an ideal HCP cell, there is a definite ratio of $c/a$ .

The Hexagonal Close-Packed c/a ratio

If you look at the central atom in the primitive cell, you can meet that it has a distance $a$ between the atoms in the airplane above and in the plane below. If you projected the cantlet into one of those planes, it would be exactly in the middle of 3 atoms.

This position is the center of the equilateral triangle. If you're a big-time nerd and y'all already know how to calculate the centroid of an equilateral triangle, go along reading.

Otherwise, click this push.

Let's draw a line betwixt the eye of the triangle and one of its corners. We tin call this $d$ . Because the angles of an equilateral triangle are all sixty°, the angle between $d$ and $\frac{a}{2}$ is 30°.

$\cos\left(30^{\circ} \right)=\frac{\left(\frac{a}{2}\right)}{d}$

And so

$d=\frac{a}{\sqrt{3}}$

Now we can make another triangle, between $d$ , $\frac{c}{2}$ , and $a$ .

$\left(d\right)^2+\left(\frac{c}{2}\right)^2=a^2$

$\left(\frac{a}{\sqrt{3}}\right)^2+\left(\frac{c}{2}\right)^2=a^2$

Which ways that

$c=\sqrt{\frac{8}{3}}a$

$\frac{c}{a}\approx 1.633$

And remembering that $a=2r$ ,

$c=4\sqrt{\frac{2}{3}}$

Now that we accept $a$ and $c$ , nosotros can summate the volume of the hexagonal unit cell.

Hexagonal Close-Packed Unit of measurement Cell Volume

The hexagonal unit prison cell is but a hexagonal prism. You can google or memorize the answer quite hands, merely in a test you might get extra points for deriving the result yourself.

Click here to encounter one method.

Start by breaking this into parts. The volume of the hexagonal prism volition be the surface area of the hexagon * the tiptop of the prism. The area of the hexagon is simply six equilateral triangles.

Allow'south get-go by computing the expanse of a single triangle. Any triangle's area is

$Area_{Triangle}=\frac{1}{2}Base\cdot Height$

Each side of the triangle has a length $a$ , so let's use that as our base. Now we need to find the superlative of the triangle.

Once again, the pythagorean theorem saves the twenty-four hours! Nosotros can brand right triangle between $\frac{a}{2}$ , $a$ , and the height $h$ .

$\left(\frac{a}{2}\right)^2+h^2=a^2$

Which means

$h=\sqrt{a^2-\left(\frac{a}{2}\right)^2}$

So the area of the triangle is

$Area_{Triangle}=\frac{a}{2}\sqrt{a^2-\left(\frac{a}{2}\right)^2}=\sqrt{\frac{3}{4}}a^2$

And since there are 6 equilateral triangles per hexagon,

$Area_{Hexagon}=6Area_{Triangle}=\frac{3\sqrt{3}}{2}$

Multiplying this expanse by the height gives

$Volume_{HCP\:cell}=\frac{3\sqrt{3}}{2}a^2c$

and using $c=\sqrt{\frac{8}{3}}a$ and $a=2r$ ,

$Volume_{HCP\:cell}=24\sqrt{2}r^3$

Now that we know the volume of the HCP unit of measurement cell, we tin can summate information technology'due south APF!

Hexagonal Shut-Packed Atomic Packing Fraction

The hard part is behind us. The atomic packing fraction (APF) is but the amount of atom inside the unit cell, compared to the overall size of the unit cell.

For the HCP jail cell, in that location are 12 corner atoms. Each corner atom has ⅙ of its volume inside the unit cell. To visualize this, imagine that you joined many unit cells together. Each corner atom would be shared between half-dozen other cells, so it contributes ⅙ to each.

There are 2 atoms on the face up, which each contribute ½ of their volume.

There are iii atoms in the center, which fully contribute their book to the unit jail cell.

Altogether, that's 6 atoms per unit cell!

We know the volume of a sphere and we already calculated the volume of the unit of measurement cell, so

$APF_{HCP}=\frac{\left(\frac{12}{6}+\frac{2}{2}+\frac{3}{1}\right)\frac{4}{3}\pi \:r^3}{24\sqrt{2}r^3}=\frac{\pi \:}{3\sqrt{2}}\approx \:74\%$

Final Thoughts

That's it! You've learned how to calculate the lattice parameters and atomic packing fraction for simple cubic (SC), trunk-centered cubic (BCC), confront-centered cubic (FCC), and hexagonal close-packed (HCP) crystal systems.

Remember, APF is just the volume of the atoms within the unit of measurement cell, divided by the total book of the unit cell. Y'all apply this to calculate the APF of any crystal organisation, even if information technology's non-cubic or has multiple kinds of atoms!